前言

神经网络中的激活函数是神经网络中至关重要的一环，它们决定了神经网络的非线性特性，能够让神经网络学习非常复杂的函数。激活函数的种类也非常丰富，从最早的 sigmoid、tanh，到后来的 ReLU、LeakyReLU、ELU 等，再到最近的 GELU、SE-ReLU、SiLU 等，每种激活函数都有其独特的优点和适用场景。

在本篇文章中，我们将对神经网络中常见的激活函数进行总结和介绍，同时也会介绍一些新兴的激活函数，帮助读者了解它们的特点和使用方法，以便在实际应用中能够选择合适的激活函数来提升神经网络的性能。

常见的激活函数

以下是一些常见的激活函数：

• Sigmoid
• Tanh
• ReLU
• LeakyReLU
• ELU

新兴的激活函数

以下是一些新兴的激活函数：

• GELU
• SE-ReLU
• SiLU

概述

神经网络中的激活函数是非常重要的组成部分，它的作用是将神经元的输入信号转换为输出信号，从而实现神经网络的非线性映射。激活函数的意义在于它能够引入非线性特性，使得神经网络可以拟合非常复杂的函数，从而提高了神经网络的表达能力和预测性能。

具体来说，激活函数的作用有以下几个方面：

1. 引入非线性特性：激活函数能够将神经元的输入信号转换为输出信号，从而引入非线性特性，使得神经网络可以拟合非常复杂的函数。
2. 压缩输出范围：激活函数能够将神经元的输出范围压缩到一定的范围内，这有助于防止神经元输出的值过大或过小，从而提高了神经网络的稳定性和泛化性能。
3. 增加网络深度：激活函数能够增加神经网络的深度，从而提高了神经网络的表达能力和预测性能。
4. 改善梯度消失问题：激活函数能够改善神经网络中的梯度消失问题，从而提高了神经网络的训练效率和收敛速度。

特性

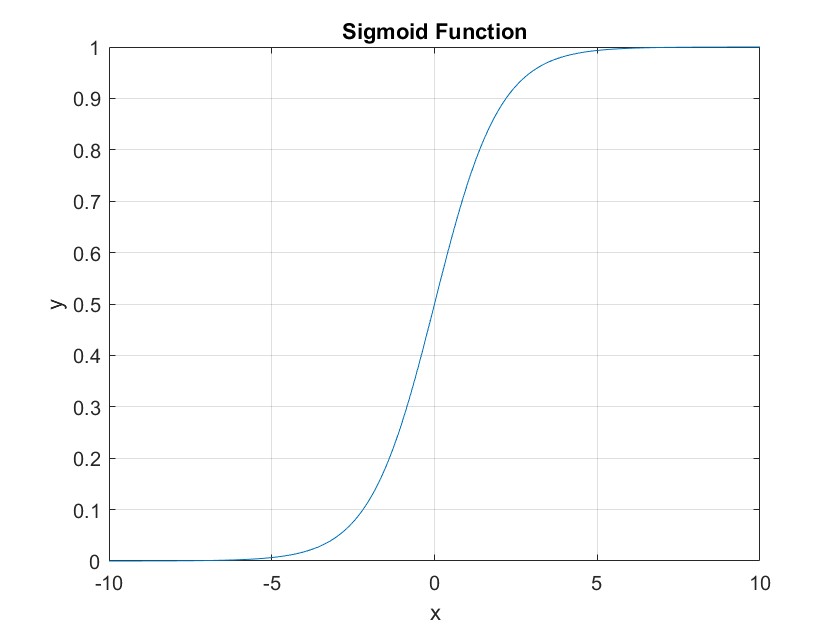
sigmoid 函数

sigmoid 函数是神经网络中最早也是最常用的激活函数之一，它的特点是将输入值映射到 0 到 1 之间的连续范围内，输出值具有良好的可解释性，但是它在梯度消失和输出饱和等问题上表现不佳。

def sigmoid(x):
    return 1. / (1. + np.exp(-x))

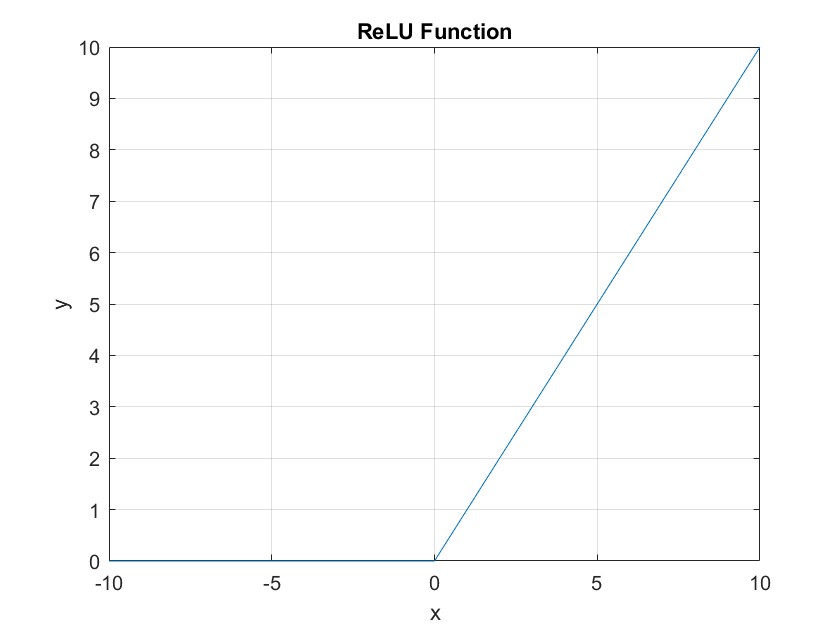
ReLU 函数

ReLU 函数是当前最常用的激活函数之一，它的特点是简单、快速，并且在许多情况下表现出色。ReLU 函数将负数输入映射到 0，将正数输入保留不变，因此在训练过程中可以避免梯度消失的问题。但是 ReLU 函数在输入为负数时输出为 0，这可能导致神经元死亡，因此后续的改进版本 LeakyReLU 得到了广泛的应用。

def ReLU(x):
    return np.maximum(0, x)

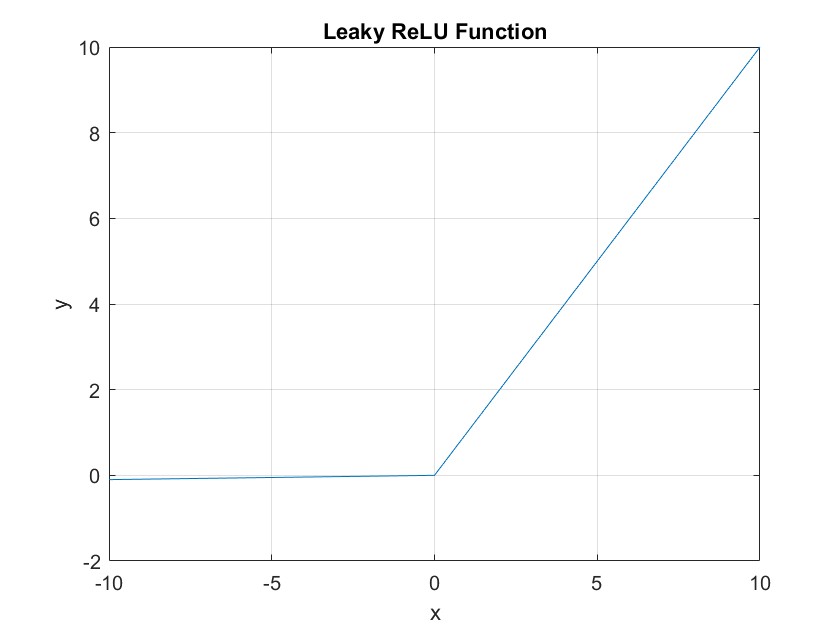
LeakyReLU 函数

LeakyReLU 函数是 ReLU 函数的改进版本，它在输入为负数时输出一个小的负数，从而避免了 ReLU 函数可能导致神经元死亡的问题。LeakyReLU 函数的优点是简单、快速，并且在许多情况下表现出色，但是其超参数需要手动调整，因此在实际应用中需要进行一定的调试。

def LeakyReLU(x, alpha=0.1):
    return np.maximum(alpha*x, x)

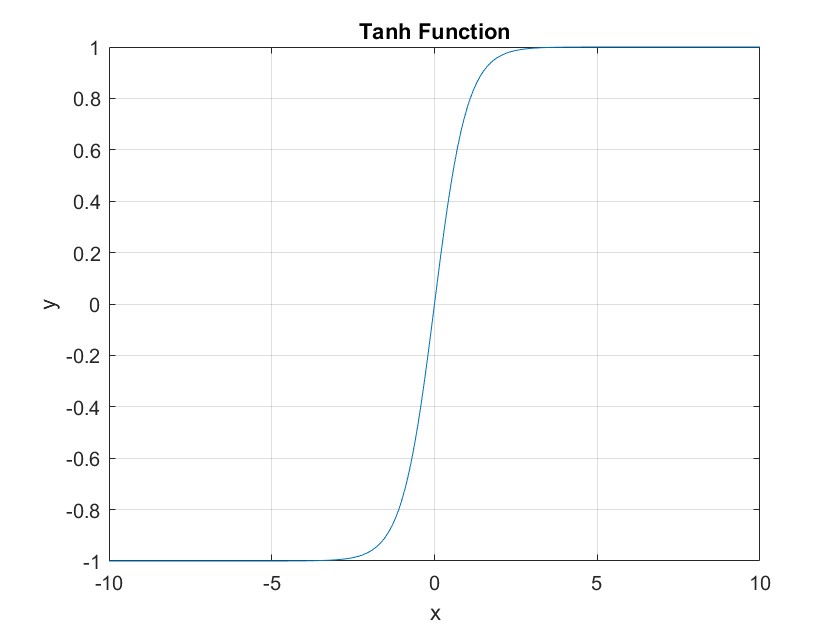
Tanh 函数

Tanh 函数是一种具有 S 形状的激活函数，其特点是将输入值映射到-1 到 1 之间的连续范围内，输出值也具有良好的可解释性。Tanh 函数在某些情况下可以表现出色，但是它也存在梯度消失和输出饱和等问题，因此在深度神经网络中使用并不广泛。

def Tanh(x):
    return np.tanh(x)

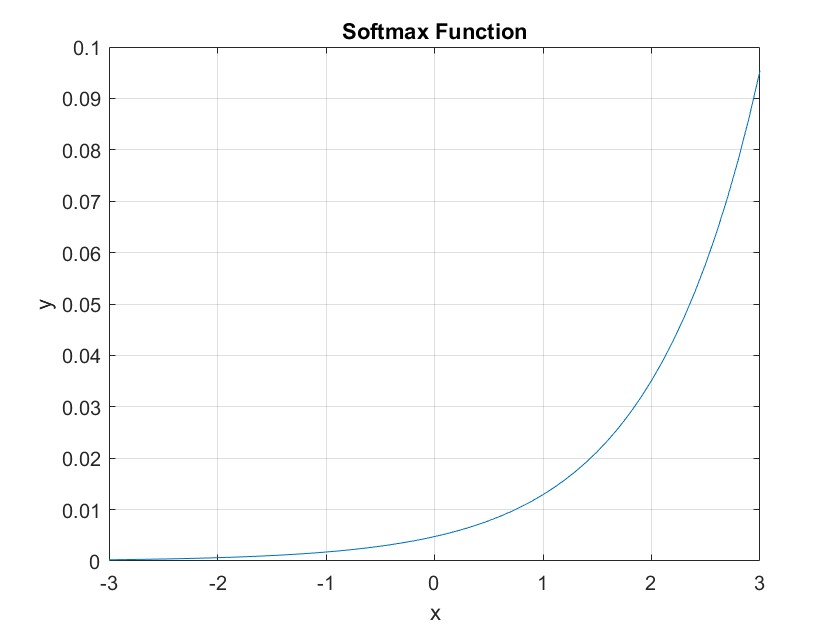
Softmax 函数

Softmax 函数是一种常用于多分类问题的激活函数，它将输入值映射到 0 到 1 之间的概率分布，可以将神经网络的输出转换为各个类别的概率值。Softmax 函数的优点是简单、易于理解，并且在多分类问题中表现出色，但是它也存在梯度消失和输出饱和等问题。

def Softmax(x):
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x, axis=0, keepdims=True)

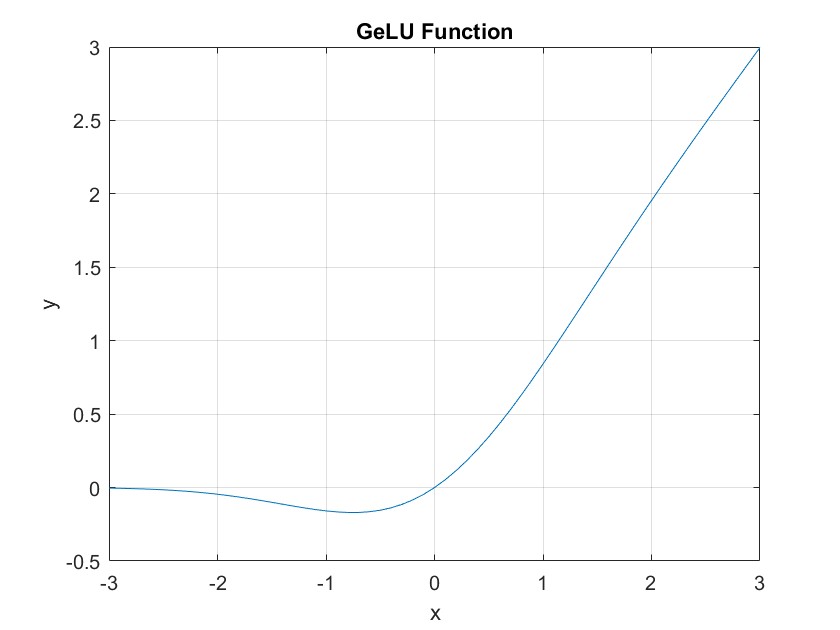
GELU 函数

GELU 函数是一种近年来提出的激活函数，它的特点是在 ReLU 函数的基础

上引入了高斯误差线性单元，从而在某些情况下能够表现出色。GELU 函数具有平滑的非线性特性，可以避免 ReLU 函数可能导致的神经元死亡问题。

def GELU(x):
    cdf = 0.5 * (1.0 + np.tanh((np.sqrt(2 / np.pi) * (x + 0.044715 * np.power(x, 3)))))
    return x * cdf

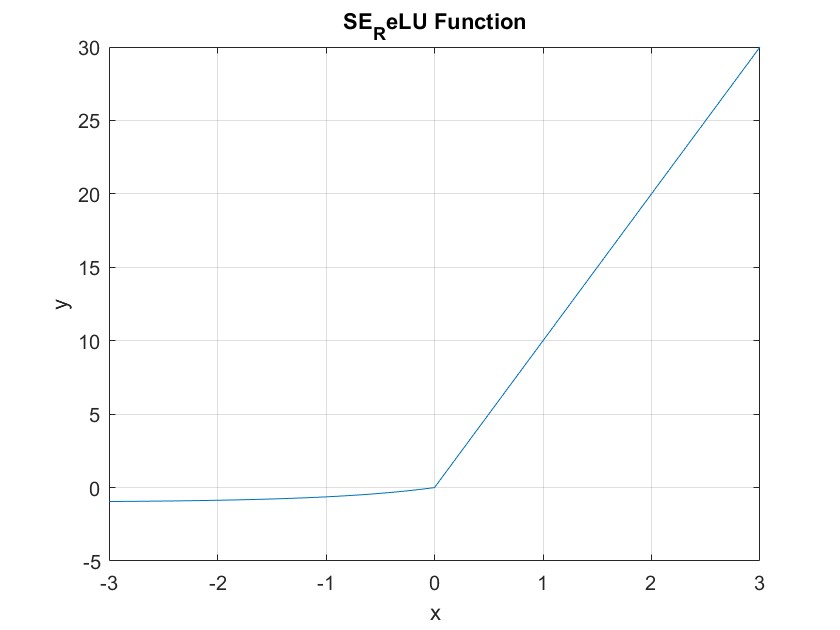
SE_ReLU 函数

SE_ReLU 函数是一种近年来提出的激活函数，它的特点是在 ReLU 函数的基础上引入了 Sigmoid 函数和 Exponential 函数，从而能够增加神经元的表达能力。SE_ReLU 函数具有非常好的平滑性和可解释性。

def SE_ReLU(x, alpha=0.1, beta=10):
    return np.where(x > 0, x + alpha * x * np.exp(-beta * x), x)

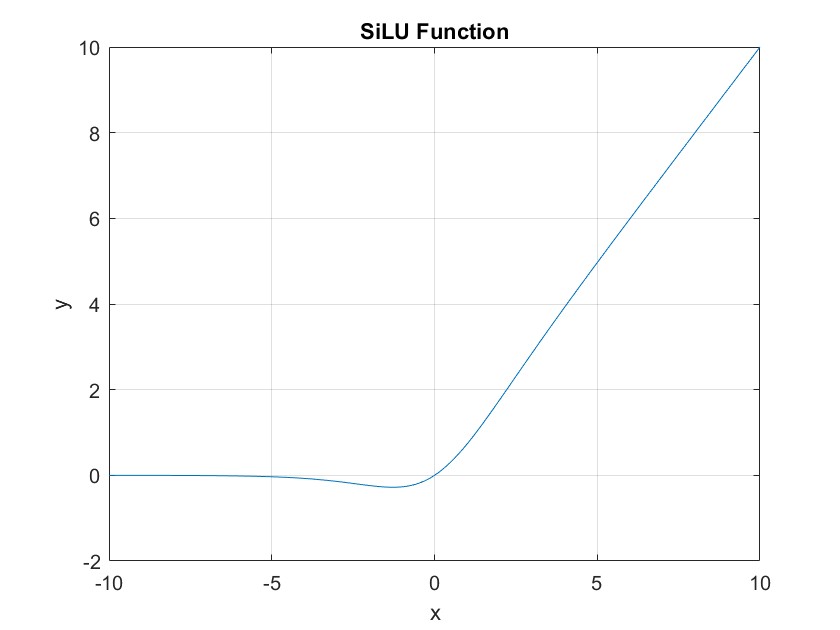
SiLU 函数

SiLU 函数是一种近年来提出的激活函数，它的特点是在 sigmoid 函数的基础上引入了自身的输入，从而能够表现出更好的非线性特性。SiLU 函数具有非常好的平滑性和可解释性。

def SE_ReLU(x, alpha=0.1, beta=10):
    return np.where(x > 0, x + alpha * x * np.exp(-beta * x), x)

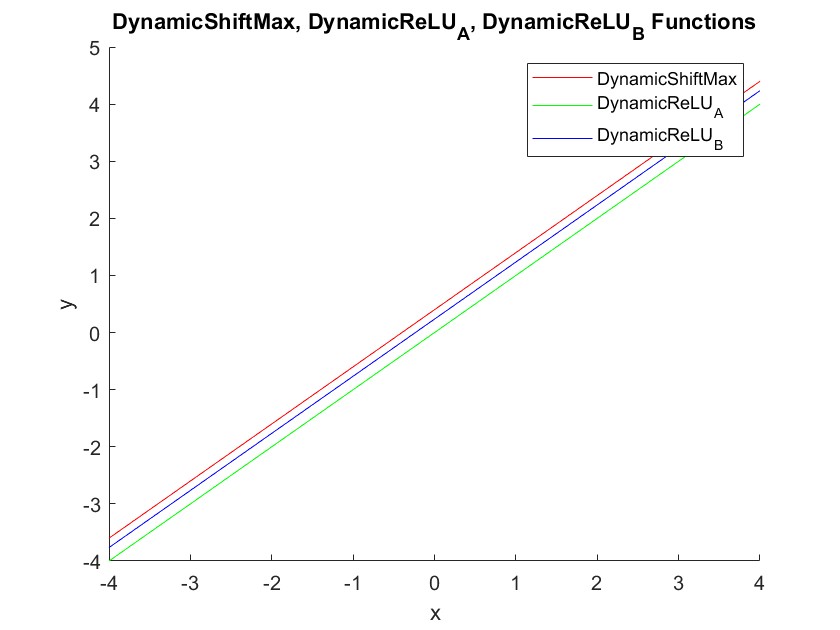
DynamicShiftMax & DynamicReLU_A & DynamicReLU_B 函数

DynamicShiftMax 函数是一种近年来提出的激活函数，它的特点是在 ReLU 函数的基础上引入了动态偏移量，从而能够增加神经元的表达能力。

def DynamicShiftMax(x, alpha=0.1):
    return np.maximum(x, x + alpha * np.max(x, axis=0, keepdims=True))

def DynamicReLU_A(x, alpha=0.1):
    return np.maximum(x, x + alpha * np.mean(x, axis=0, keepdims=True))

def DynamicReLU_B(x, alpha=0.1):
    return np.maximum(x, x + alpha * np.std(x, axis=0, keepdims=True))

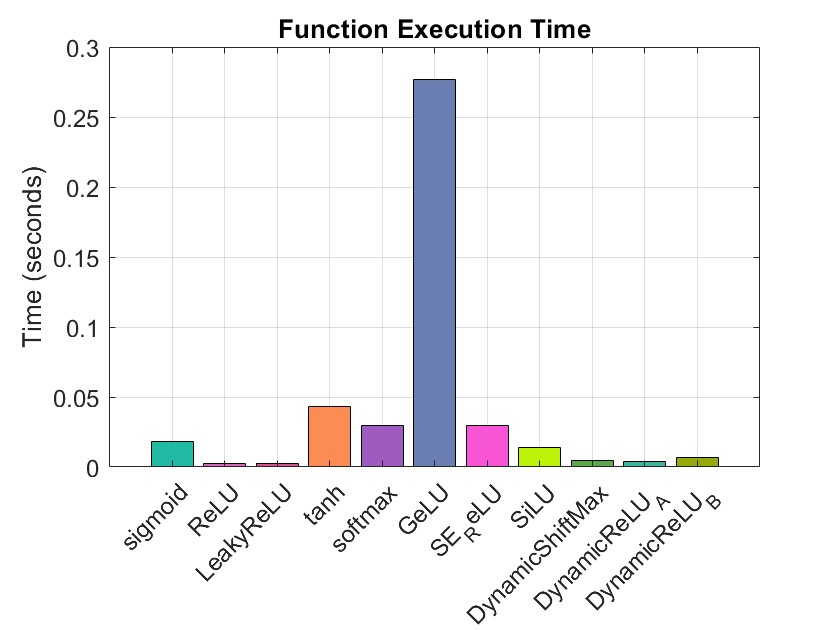
性能测试

我们采用控制变量法进行激活函数的推理速度测试，x 为输入，范围为-1 到 1 之间的十万个数据，运行次数为 100 计算激活函数的计算耗时。

if __name__ == "__main__":
    x = np.linspace(-1, 1, 100000)
    t1 = time.time()
    for i in range(100):
        y = sigmoid(x)
    t2 = time.time()
    print(float(t2 - t1))

完整代码如下

import numpy as np
import time
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1. / (1. + np.exp(-x))

def ReLU(x):
    return np.maximum(0, x)

def LeakyReLU(x, alpha=0.1):
    return np.maximum(alpha * x, x)

def Tanh(x):
    return np.tanh(x)

def Softmax(x):
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x, axis=0, keepdims=True)

def GELU(x):
    cdf = 0.5 * (1.0 + np.tanh((np.sqrt(2 / np.pi) * (x + 0.044715 * np.power(x, 3)))))
    return x * cdf

def SE_ReLU(x, alpha=0.1, beta=10):
    return np.where(x > 0, x + alpha * x * np.exp(-beta * x), x)

def SE_ReLU(x, alpha=0.1, beta=10):
    return np.where(x > 0, x + alpha * x * np.exp(-beta * x), x)

def DynamicShiftMax(x, alpha=0.1):
    return np.maximum(x, x + alpha * np.max(x, axis=0, keepdims=True))

def DynamicReLU_A(x, alpha=0.1):
    return np.maximum(x, x + alpha * np.mean(x, axis=0, keepdims=True))

def DynamicReLU_B(x, alpha=0.1):
    return np.maximum(x, x + alpha * np.std(x, axis=0, keepdims=True))

name = [sigmoid, ReLU, LeakyReLU, Tanh, Softmax, GELU, SE_ReLU, DynamicShiftMax, DynamicReLU_A, DynamicReLU_B]

if __name__ == "__main__":
    x = np.linspace(-1, 1, 1000000)
    times = []  # 创建一个空列表来存储函数名称和时间
    for n in name:
        t1 = time.perf_counter()  # 使用perf_counter
        y = n(x)
        t2 = time.perf_counter()  # 使用perf_counter
        times.append((n.__name__, float(t2 - t1)))  # 将函数名称和时间作为元组添加到列表中

    for n, t in times:  # 遍历列表并打印每个函数名称和时间
        print(f'{n}: {t}')

# 用plot绘制times列表中的数据
plt.figure(figsize=(10, 5))
plt.bar(*zip(*times)) # 使用zip(*times)将元组列表转换为两个元组列表
plt.ylabel('Time (s)')
plt.title('Activation Functions')
plt.show()